Калькуляторы расчета размеров развертки конуса

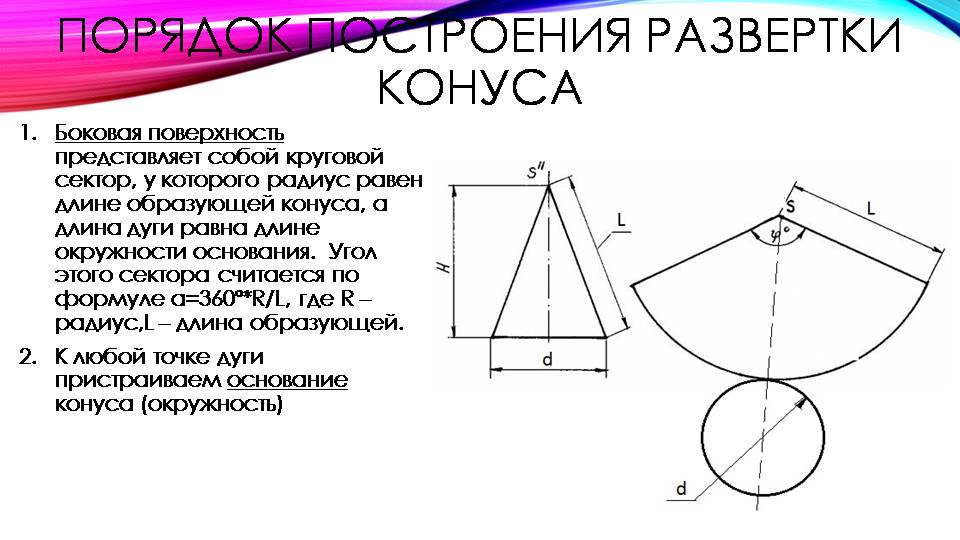
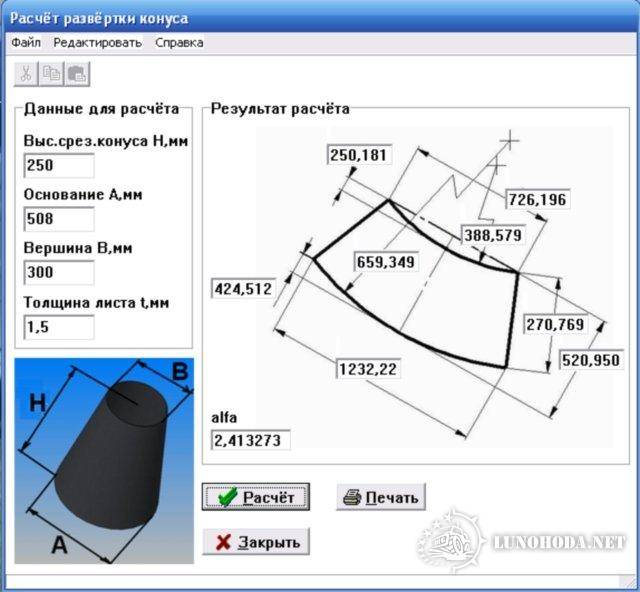
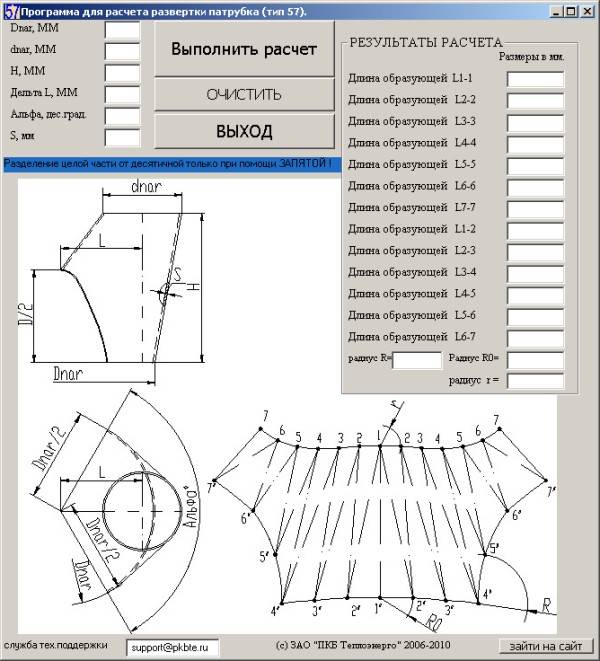
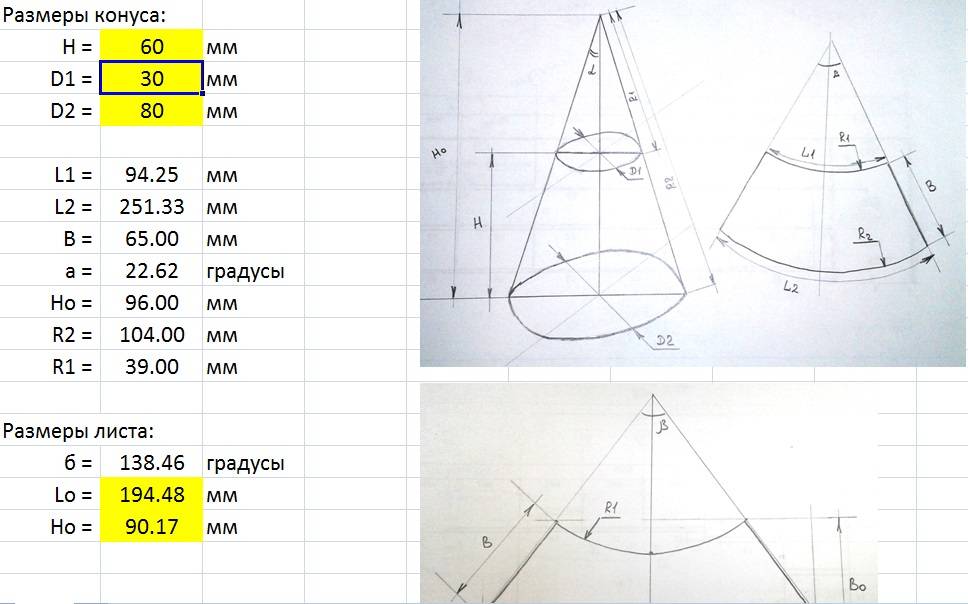
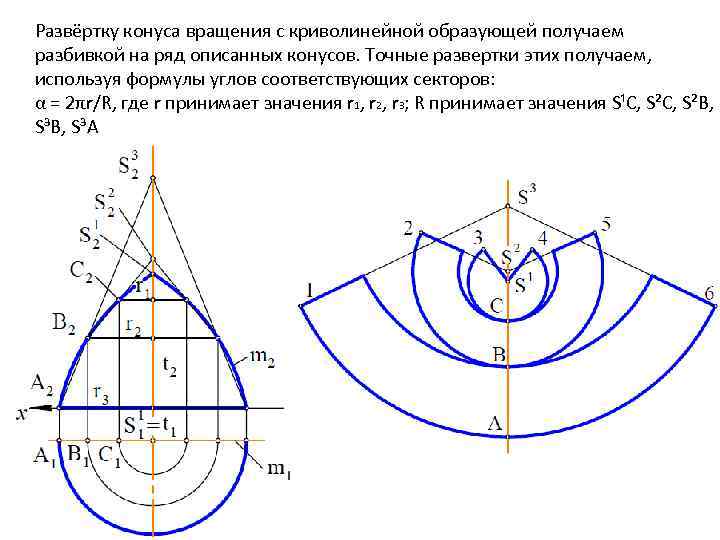
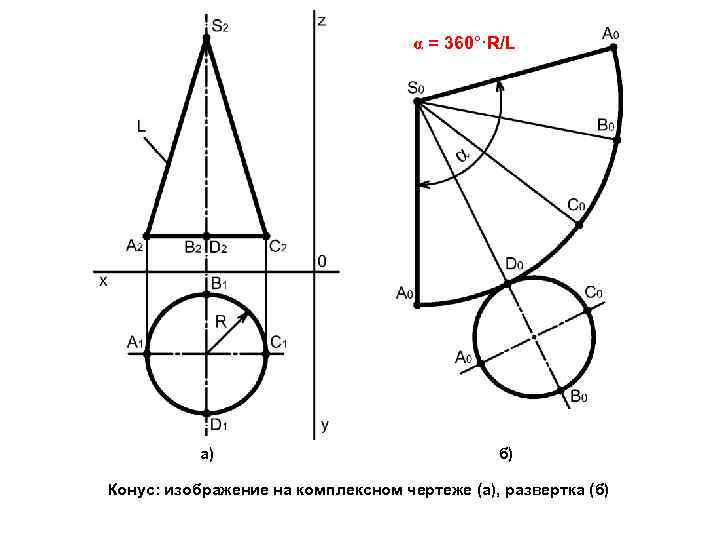
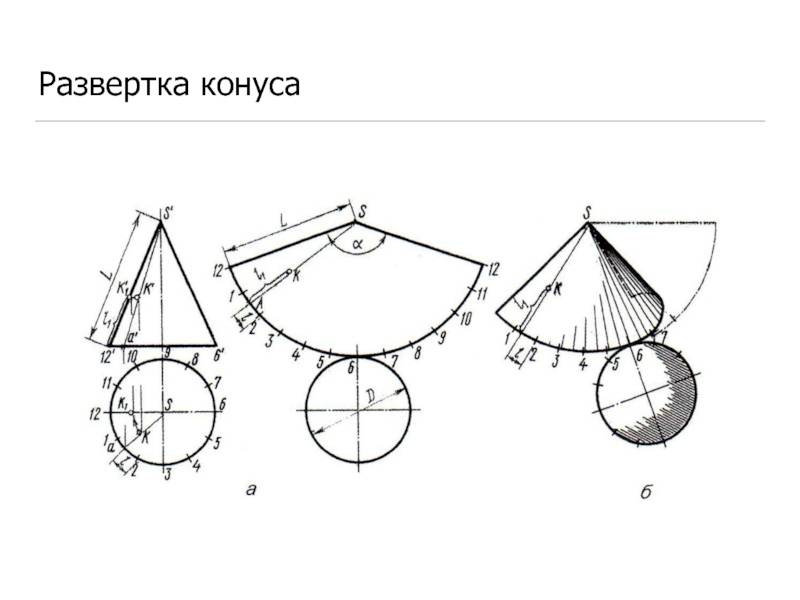
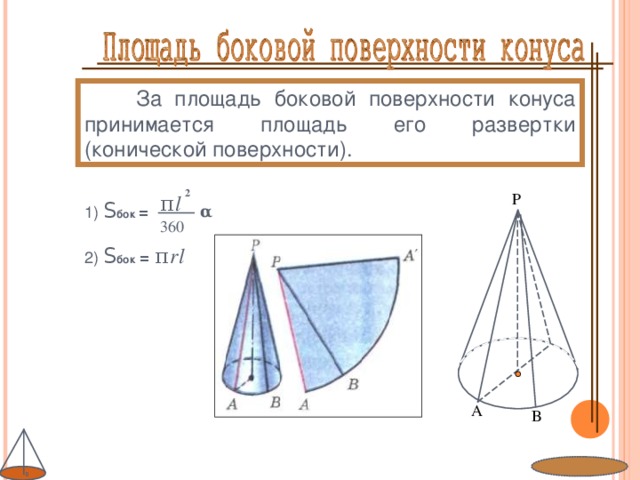
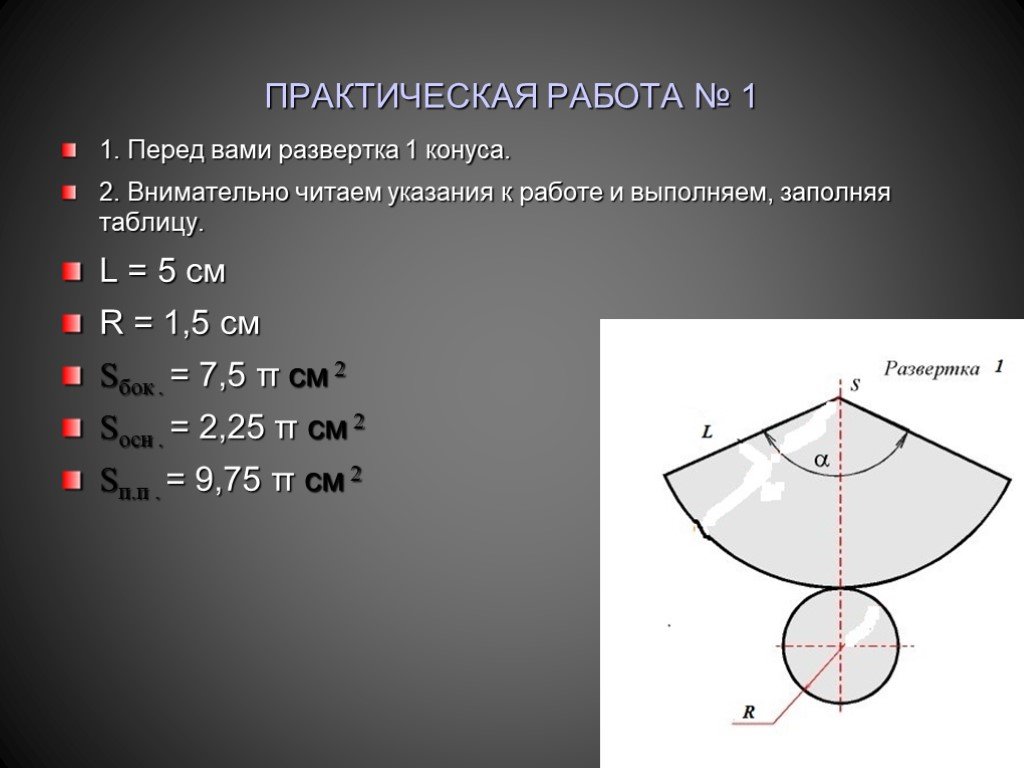
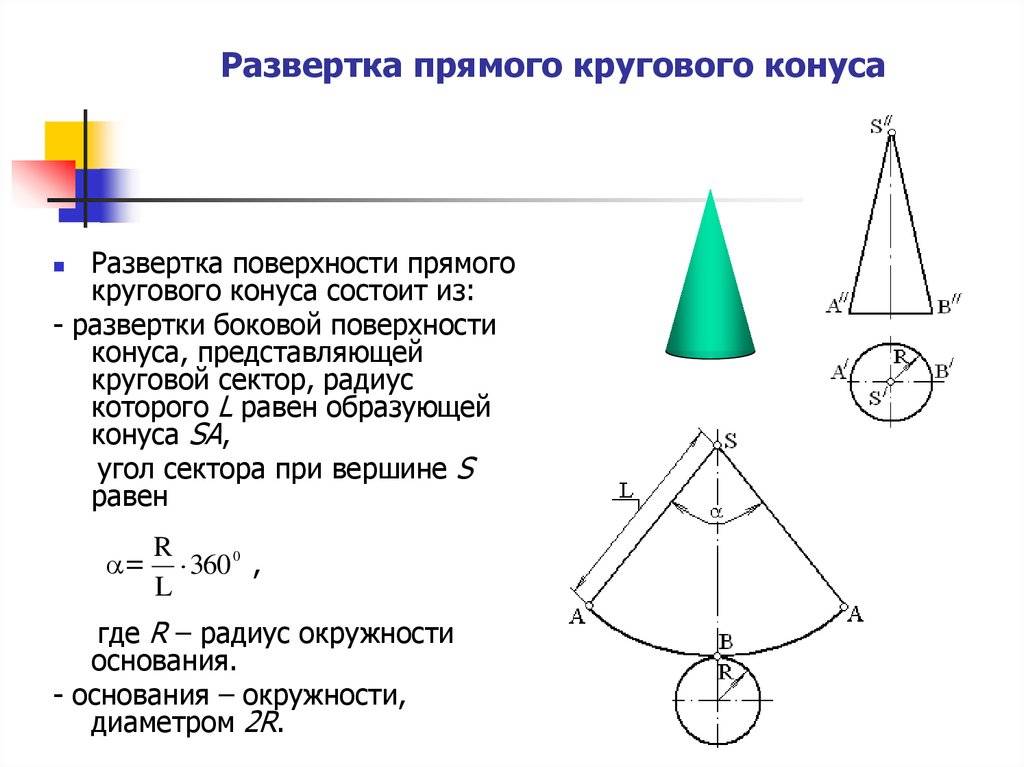
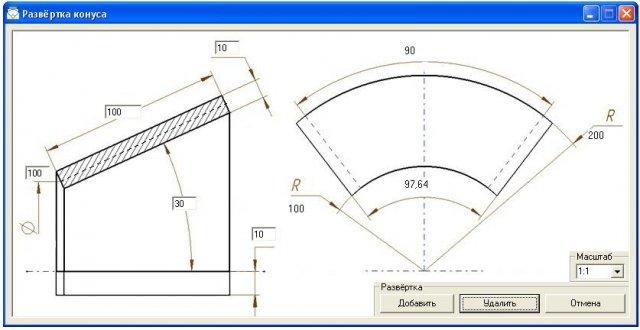
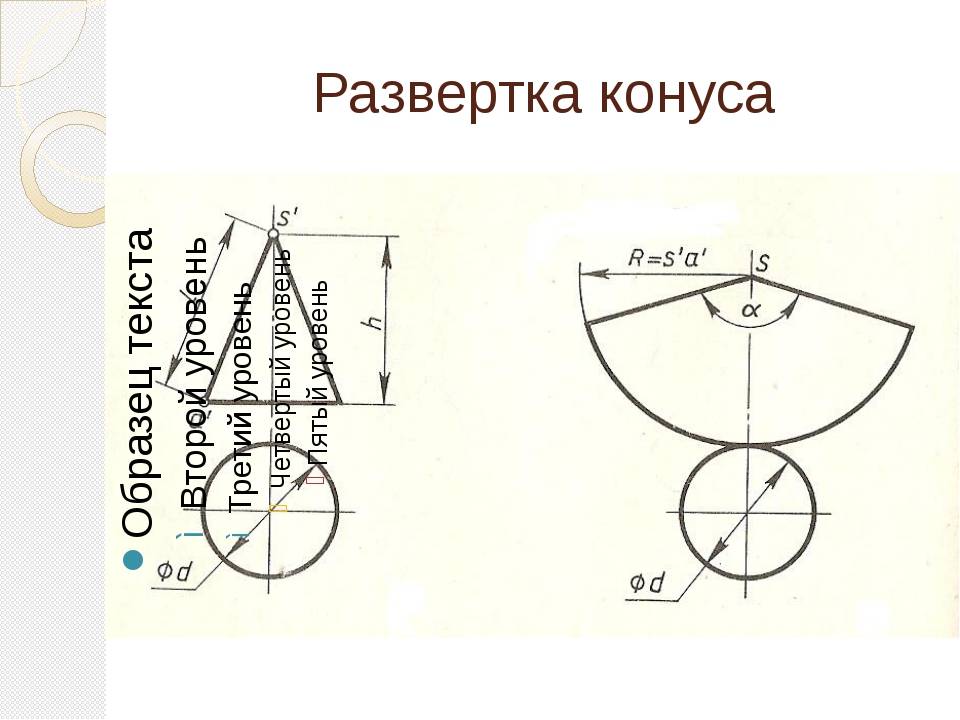
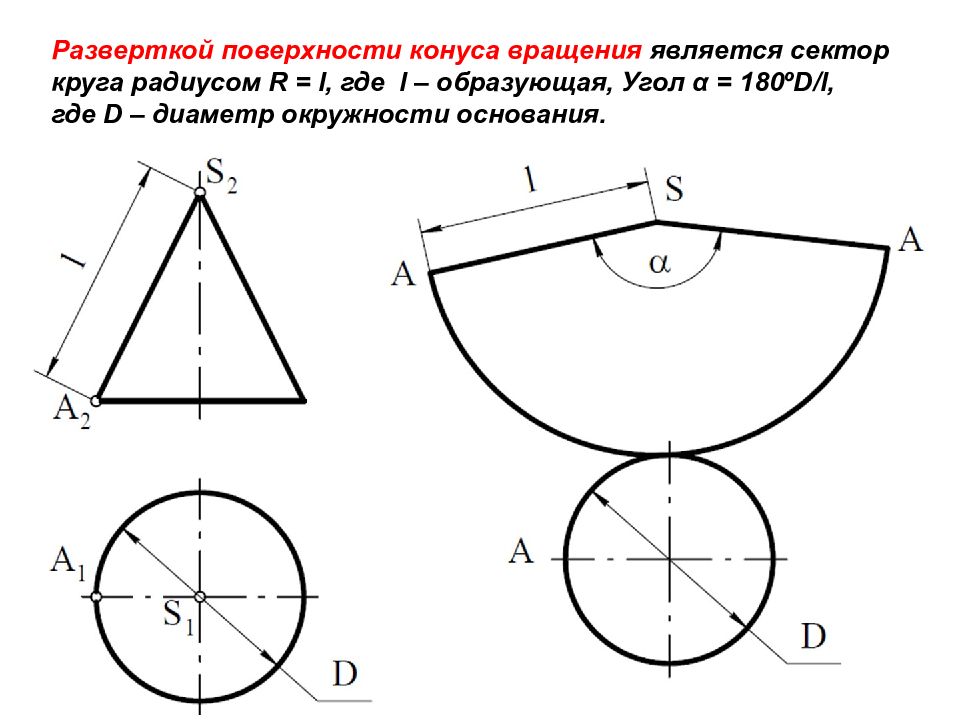
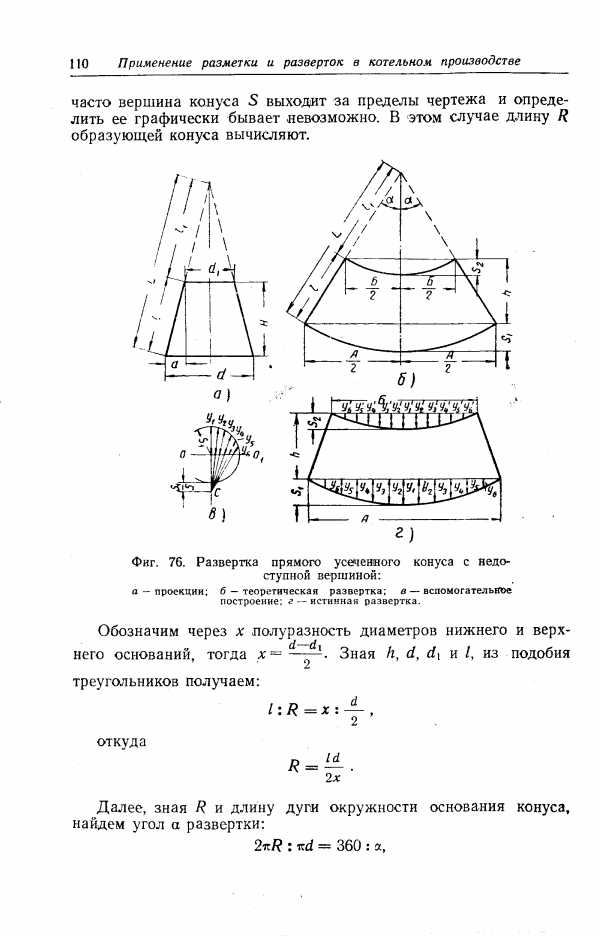
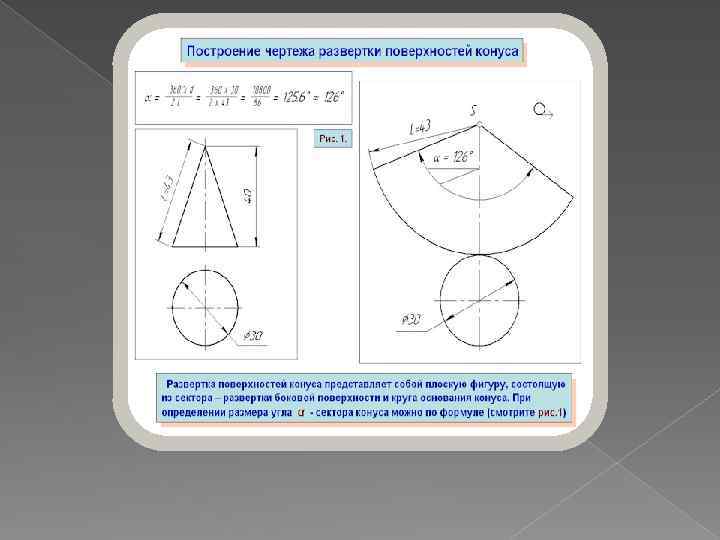
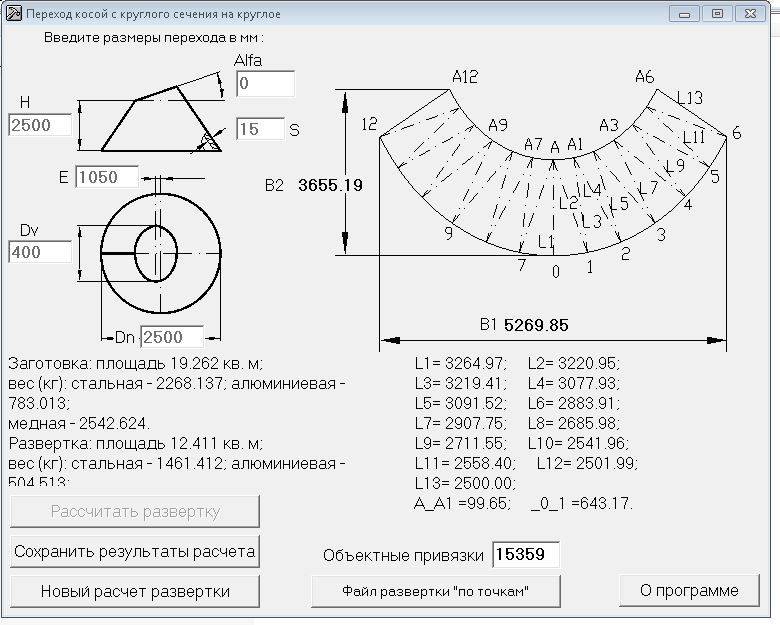
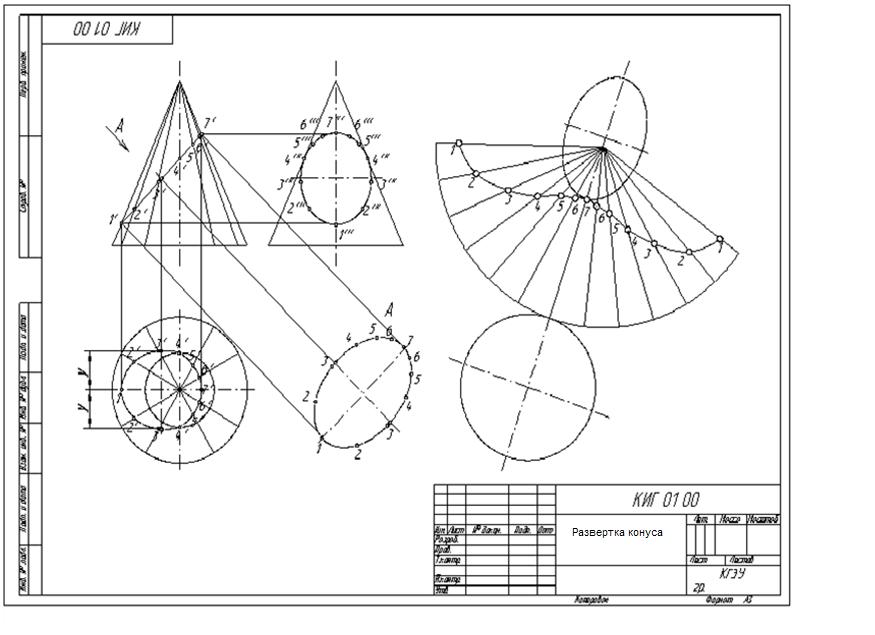
Развертка (выкройка) конуса

• Следующий уникальный калькулятор служит для перевода экзотических единиц длины в…
• Следующий онлайн калькулятор о фунтах. Ранее он был очень популярен,…
• Следующий онлайн калькулятор может вычислить уровень жидкости в цилиндрической таре…
• Следующий онлайн калькулятор переводит температуры между разными шкалами. Помните калькулятор…
• Следующий калькулятор интересен тем, что он переводит древние российские денежные…
• Следующий калькулятор будет очень полезен тем, кто решил купить или…
• Следующий калькулятор работает очень просто, вам нужно ввести всего одно…
• Следующий онлайн калькулятор считает рост человека благодаря русской системе мер…
• Следующий онлайн калькулятор может вычислить габариты экрана телевизоров, компьютеров, проекторов,…
• Перед вами 2 калькулятора: один поможет вам подобрать формат снимков…
• Следующие 2 калькуляторы переводят заданное число плиток в квадратные метры…
• Перед вами 2 онлайн-калькулятора. Они переводят меры площади из метрической…
• Следующий необычный калькулятор переводит меры длины из русской системы в…
• Перед вами 2 калькулятора, которые предназначены для перевода мер длины…
• Следующий простенький калькулятор переводит введенную вами toC из кельвинов в…
• Следующий калькулятор предназначен для перевода кг в фунты. Также есть…
• Следующий онлайн калькулятор переводит калибр древних артиллерийских орудий из фунтов…
• Давайте вспомним калькулятор, который переводит градусы Цельсия в градусы Фаренгейта:…
• Как вы уже могли заметить на нашем сайте есть несколько…
• Следующий уникальный калькулятор переводит градусы Цельсия в градусы Фаренгейта. Наверное,…
• Следующий калькулятор умеет переводить значение угла, которое задано в градусах,…
• Следующий калькулятор делает перевод единиц измерения углов из градусов, минут,…
• Следующий калькулятор делает расчет объема сегмента цилиндра. Давайте посмотрим каким…
• Следующий онлайн-калькулятор считает объем жидкости в бочке, которая имеет цилиндрическую…
• Следующий калькулятор служит для детального подсчета суммарной работы аппарата. Вам…
• Перед вами отличный помощник для IT специалистов. С помощью данного…
• Следующий калькулятор переводит числа, записанные римскими цифрами в простые десятичные…
• Следующий калькулятор переводит скорость из м/с в км/час. Часто при…
• Начнем с истории. В 17 веке итальянским ученым Торричелли было…
• Следующий онлайн-калькулятор рассчитывает параметры горловины для цилиндрического бочки. Все работает…

hostciti.net

Усеченный конус и способы его получения

Предположим, что у нас имеется фигура, которая была показана в предыдущем пункте. Возьмем плоскость, параллельную основанию конуса, и отсечем с помощью нее вершину фигуры. Этот процесс показан на рисунке.

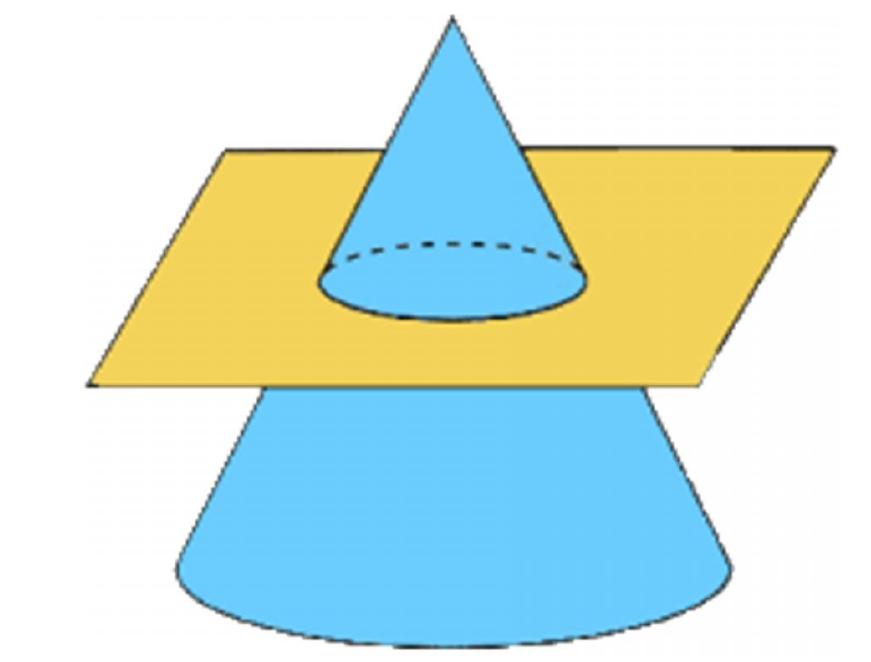
Образованная над плоскостью фигура является конусом, а вот фигура под плоскостью — это конус усеченный.

Существует еще один способ получения рассматриваемой фигуры. Предположим, что имеется некоторая трапеция с двумя прямыми углами. Если вращать эту трапецию вокруг стороны, к которой прямые углы прилегают, то она опишет поверхность усеченного конуса. Этот способ получения фигуры демонстрирует схема ниже.

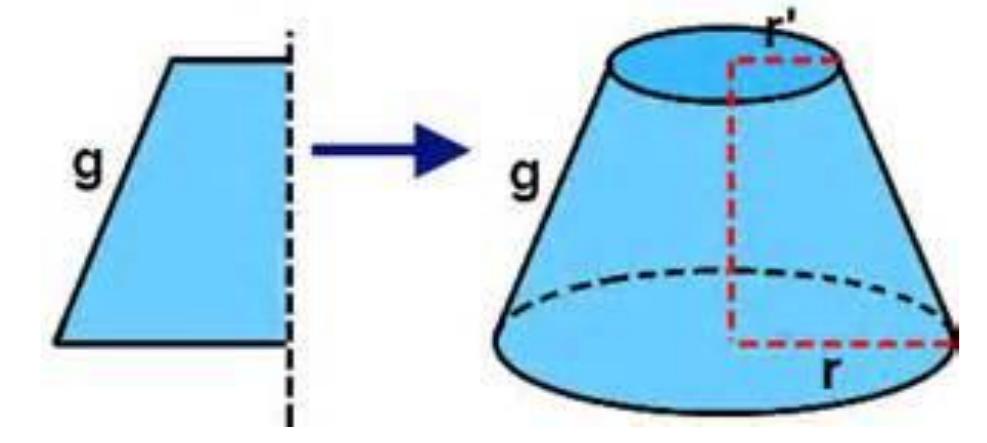
Сторона трапеции, вокруг которой выполнялось вращение, будет являться осью усеченного конуса. Отрезок, который на оси отсекают два основания фигуры, называется высотой. На рисунке отмечены образующая g и радиусы оснований конуса усеченного r и r’.

Наконец, третий способ получения усеченного конуса заключается в увеличении количества ребер усеченной пирамиды до бесконечного числа. Во время этого процесса пирамида постепенно перейдет в конус.

Любопытно отметить, что форма рассматриваемой геометрической фигуры в первом приближении в природе характерна для действующего вулкана, что отчетливо видно на следующей фотографии.

Выкройка для конуса

Главная > Геометрия > Выкройка для конуса

19.11.2012 // Владимир Трунов

Вместо слова «выкройка» иногда употребляют «развертка», однако этот термин неоднозначен: например, разверткой называют инструмент для увеличения диаметра отверстия, и в электронной технике существует понятие развертки. Поэтому, хоть я и обязан употребить слова «развертка конуса», чтобы поисковики и по ним находили эту статью, но пользоваться буду словом «выкройка».

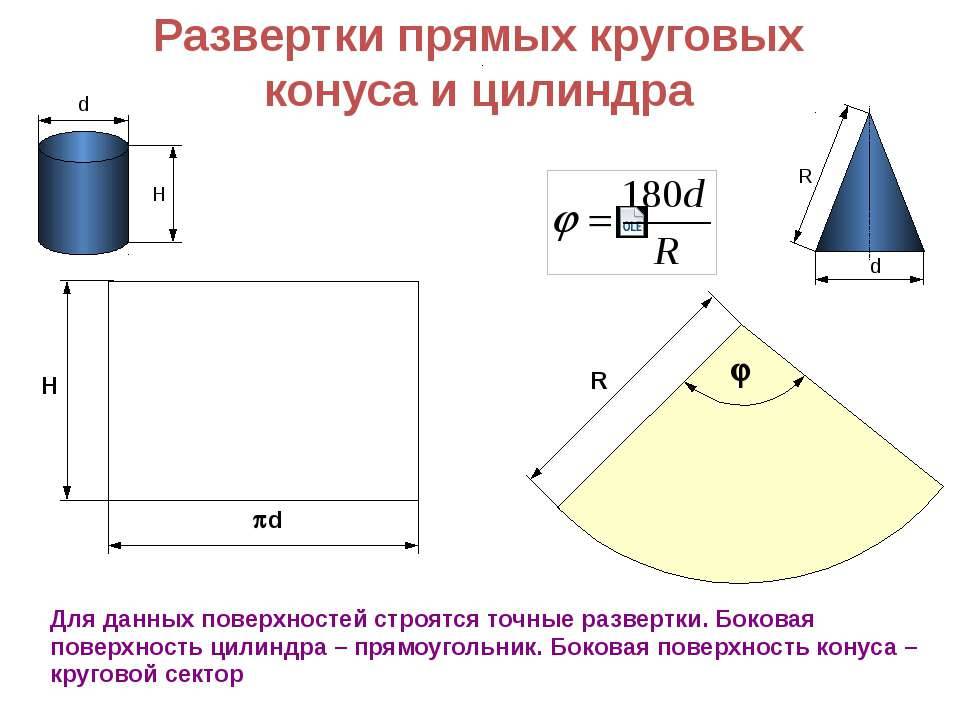
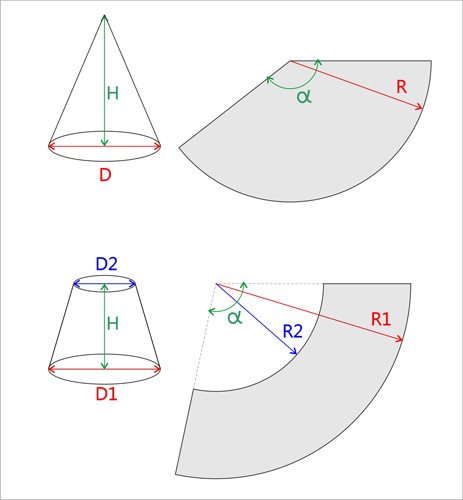
Построение выкройки для конуса — дело нехитрое. Рассмотрим два случая: для полного конуса и для усеченного. На картинке (кликните, чтобы увеличить) показаны эскизы таких конусов и их выкроек. (Сразу замечу, что речь здесь пойдет только о прямых конусах с круглым основанием. Конусы с овальным основанием и наклонные конусы рассмотрим в следующих статьях).

Полный конус

Обозначения:

• — диаметр основания конуса;
• — высота конуса;
• — радиус дуги выкройки;
• — центральный угол выкройки.

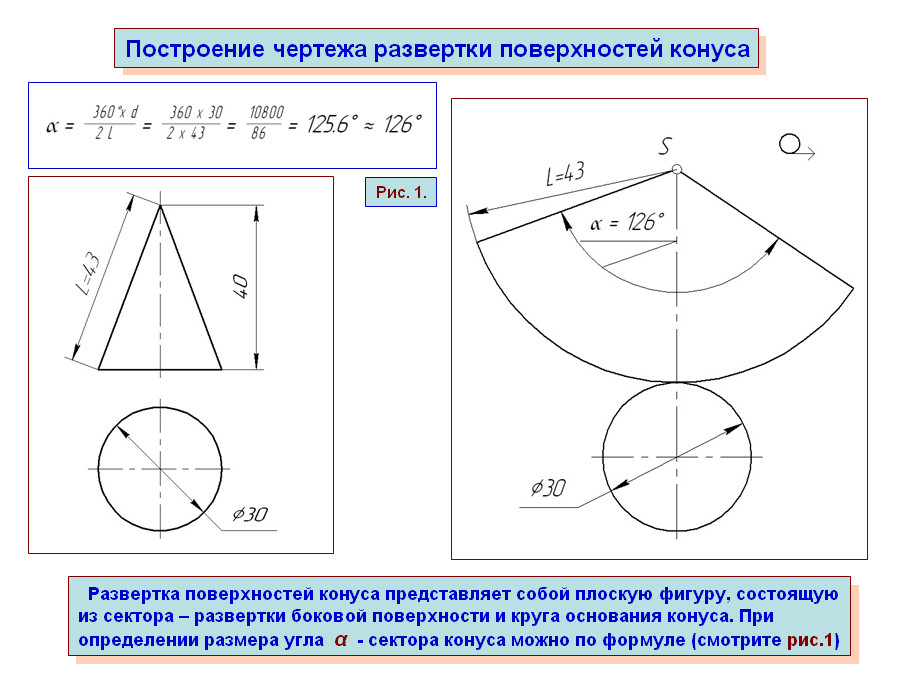
Параметры выкройки рассчитываются по формулам: ; ; где .

Усеченный конус

Обозначения:

• — диаметр большего основания конуса;
• — диаметр меньшего основания конуса;
• — высота конуса;
• — радиус внешней дуги выкройки;
• — радиус внутренней дуги выкройки;
• — центральный угол выкройки.

Формулы для вычисления параметров выкройки: ; ; ; где . Заметим, что эти формулы подойдут и для полного конуса, если мы подставим в них .

Угол при вершине конуса

Иногда при построении конуса принципиальным является значение угла при его вершине (или при мнимой вершине, если конус усеченный). Самый простой пример — когда нужно, чтобы один конус плотно входил в другой. Обозначим этот угол буквой (см. картинку). В этом случае мы можем его использовать вместо одного из трех входных значений: , или . Почему «вместо«, а не «вместе«? Потому что для построения конуса достаточно трех параметров, а значение четвертого вычисляется через значения трех остальных. Почему именно трех, а не двух и не четырех — вопрос, выходящий за рамки этой статьи. Таинственный голос мне подсказывает, что это как-то связано с трехмерностью объекта «конус». (Сравните с двумя исходными параметрами двухмерного объекта «сегмент круга», по которым мы вычисляли все остальные его параметры в статье Геометрия круга.)

Ниже приведены формулы, по которым определяется четвертый параметр конуса, когда заданы три.

• Заданы ; тогда .
• Заданы ; тогда .
• Заданы ; тогда .
• Заданы ; тогда .

Методы построения выкройки

• Вычислить значения на калькуляторе и построить выкройку на бумаге (или сразу на металле) при помощи циркуля, линейки и транспортира.
• Занести формулы и исходные данные в электронную таблицу (например, Microsoft Exel). Полученный результат использовать для построения выкройки при помощи графического редактора (например, CorelDRAW).
• использовать мою программу Cones, которая нарисует на экране и выведет на печать выкройку для конуса с заданными параметрами. Эту выкройку можно сохранить в виде векторного файла и импортировать в CorelDRAW.

Не параллельные основания

Что касается усеченных конусов, то программа Cones пока строит выкройки для конусов, имеющих только параллельные основания. Для тех, кто ищет способ построения выкройки усеченного конуса с не параллельными основаниями, привожу ссылку, предоставленную одним из посетителей сайта: Усеченный конус с не параллельными основаниями.

геометрические формулы

Колпак на дымоход своими руками

Хозяева домов зачастую прибегают к использованию элементов в виде различных колпаков и зонтов, служащих, как это кажется на первый взгляд, для украшения дымовых труб. В то же время такие насадки не только улучшают эстетическое восприятие строения, но и обеспечивают полезную функциональность. Обычно так называемый козырек для дымохода изготавливается собственными силами, так как для этого не требуется серьезных знаний и умений. Хотя наряду с простой конструкцией этих элементов встречаются достаточно замысловатые поделки, которые проблематично соорудить без соответствующего опыта.

Конструктивные особенности

Колпак на дымоход представляет собой устройство, предназначенное для защиты трубы от попадания влаги. Внешний вид таких козырьков может быть различен, что имеет зависимость как от предпочтений хозяина дома, так и от конфигурации трубы.

Колпаки на трубу дымохода включают в себя:

• зонтик – устанавливаемая на вершине колпака защита от осадков, посторонних предметов и проникновения птиц, внешний вид которой имеет форму пирамиды, конуса или соответствует другой геометрии;
• фартук – часть колпака, отвечающая за защиту верха трубы от стекающей с зонтика воды. Обычно установка этого элемента производится при оснащении прямоугольной или квадратной трубы. В результате гарантируется увеличение срока службы дымохода, так как удается практически исключить вероятность появления коррозии и грибка;
• кронштейны – крепежные элементы, представляющие собой металлические полоски, которые позволяют соединить козырек и фартук. Непосредственное крепление в данном случае производится за счет использования сварки.

Имейте в виду! Собрать колпак для дымохода вполне реально самому, но только в том случае, если вы хотите установить достаточно простой флюгарок. Модели, отличающиеся большей сложностью в плане конструктивных особенностей, гораздо выгоднее заказать или купить.

При наличии выбора лучше всего отдать предпочтение тем моделям, которые оборудованы открывающейся крышкой. Это позволит проводить профилактический осмотр дымохода и его чистку без каких-либо проблем, что связано с комфортом доступа.

Колпак на дымоход долгого срока использования может быть изготовлен только из железа, устойчивого к коррозии: оцинкованная сталь, алюминий и медь. В последнем случае предлагаемый металл обладает ярко выраженным декоративным характером, так как его переливы на солнце могут придать вашем дому определенную респектабельность.

Одевают оголовок на трубу дымохода чтобы гасить искры. Это одно из его предназначений. Поэтому качество железа должно быть хорошим, тем самым оно долго не прогорит.

Виды

В связи с тем, что дымоходы отличаются разнообразием форм и размеров, производители колпаков также предлагают широкий ассортимент продукции. Если вы решите украсить свое жилище и продлить срок жизни дымохода, то придется выбирать среди большого ассортимента флюгарок:

1. Стандартные – зонт на дымоход в виде пирамидки, для изготовления которой используется листовой металл, а крепление к фартуку осуществляется посредством кронштейнов.
2. Четырехскатные – устанавливается преимущественно на прямоугольные трубы, выполненные из кирпича. По форме соотносится с вальмовой крышей с четырьмя скатами.
3. С полукруглым зонтиком – визуально отличается красотой, но обеспечивает недостаточную тягу. Преимущественно используется для установки на дымоходах домов, которые построены по европейским стандартам.
4. Плоские – часто можно встретить на зданиях в стиле модерн. Имеет прямоугольную форму и отличается таким недостатком, как повышенная нагрузка на кронштейны, что в некоторых случаях приводит к их деформации. Это связано с плоской крышей колпака, которая не дает возможность скатываться снегу. Данный факт определяет возникновение упомянутой проблемы.
5. Круглые с конусообразным зонтиком – модели без капельника, устанавливаемые на выполненные из нержавейки дымоходы круглого сечения.

Гибка металла на вальцах

07 Дек 2013 Рубрика: Механика |

За последнее время ко мне было несколько обращений от читателей блога за помощью в решении одной и той же задачи: как при работе на трехвалковых листогибочных вальцах и профилегибах определить окончательное местоположение среднего ролика (валка)…

…относительно положения крайних роликов (валков), которое обеспечит гибку (вальцовку) заготовки с определенным заданным необходимым радиусом? Ответ на этот вопрос позволит повысить производительность труда при гибке металла за счет уменьшения количества прогонов заготовки до момента получения годной детали.

В этой статье вы найдете теоретическое

решение поставленной задачи. Сразу оговорюсь – на практике я этот расчет не применял и, соответственно, не проверял результативность предлагаемого метода. Однако я уверен, что в определенных случаях гибка металла может быть выполнена гораздо быстрее при использовании этой методики, чем обычно.

Круглый прямой конус и его линейные характеристики

Выше было дано общее определение, что такое конус. Тем не менее часто на практике и в геометрических задачах встречается конкретный вид этой фигуры — прямой круглый конус. Он изображен ниже на рисунке.

Основанием этой фигуры является круг. Прямым он называется потому, что перпендикуляр, опущенный на его основания с высоты, будет пересекать круг точно в его центре. Если бы это условие не выполнялось, тогда можно говорить о наклонном конусе.

Линия, которая соединяет вершину с центром круга, называется осью фигуры. Она также является осью вращения конуса. Действительно, если взять прямоугольный треугольник и начать вращать его вокруг одного из катетов, то полученная в результате вращения фигура будет конусом прямым с круглым основанием. Этот способ получения конуса схематически показан ниже на рисунке.

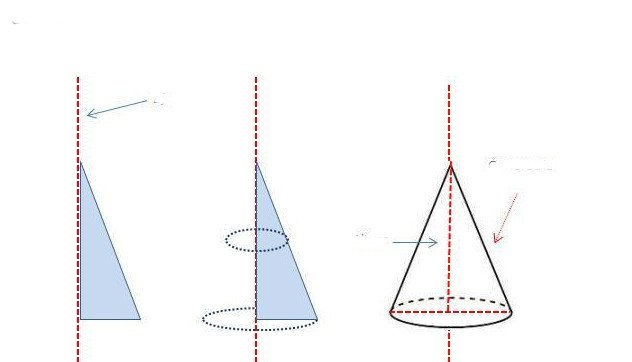
Видно, что образующая будет равна длине гипотенузы треугольника. Катет, вокруг которого осуществлялось вращение, станет высотой для объемной фигуры, а второй катет будет равен радиусу конуса (радиус круглого основания).

Одной из важных особенностей рассматриваемой фигуры является то, что длины всех образующих для нее равны друг другу. Этот факт позволяет, пользуясь теоремой Пифагора, записать математическую связь между тремя основными линейными параметрами фигуры:

Квадрат генератрисы g прямого круглого конуса равен сумме квадратов его радиуса r и высоты h.

Разобрав вопрос, что такое конус прямой с круглым основанием, покажем, как можно площадь его поверхности и объем.

Исходный полный конус

Прежде чем говорить об усеченном объекте и его характеристиках, следует рассмотреть исходную фигуру, из которой он получается.

Пусть имеется некоторая замкнутая кривая, лежащая в произвольной плоскости. Это может быть окружность, эллипс или любая другая линия с плавными перегибами. Пусть также существует отрезок, который не лежит в плоскости указанной замкнутой кривой. Если в пространстве зафиксировать некоторую точку, а затем соединить ее с любой точкой на кривой, то получится образующая будущего конуса. Если теперь ее перемещать вдоль замкнутой кривой одним своим концом, в то время как другой конец будет зафиксированным в точке, то она опишет коническую поверхность.

Это геометрическое построение позволяет получить объемную фигуру конус, которая состоит из следующих элементов:

1. Вершина — зафиксированная точка в пространстве, которая не лежит в плоскости замкнутой кривой.
2. Коническая поверхность, образованная в результате перемещения отрезка — образующей, или генератрисы.
3. Основание — часть плоскости, ограниченная исходной замкнутой кривой. Последняя является направляющей, или директрисой, для образующей.

Существующие виды

В геометрии известны несколько видов конуса. Каждый из них определяется характером директрисы и расположением относительно нее генератрисы. Выделяют следующие виды фигуры:

1. Круглый прямой. В его основании лежит круг, а высота (длина перпендикуляра, опущенного из вершины) соединяет центр окружности и вершину.
2. Эллиптический прямой. В его основании находится эллипс, а проекция вершины попадает точно в центр основания.
3. Наклонный произвольного вида. Высота в этом конусе всегда меньше, чем длина отрезка, соединяющего вершину и геометрический центр основания.

Круглая прямая фигура

Получить этот конус несложно. Необходимо взять прямоугольный треугольник, поставить его на один из катетов и вращать вокруг второго катета, который будет являться осью, а его длина — высотой для объемной фигуры. Катет, на котором стоит треугольник, является радиусом круглого основания конуса.

С полученной фигурой легко работать при решении геометрических задач, поскольку для нее существуют довольно простые формулы для площади поверхности и объема.

Площадь S фигуры состоит из двух частей: основания и боковой поверхности. С помощью простых геометрических рассуждений можно показать, что сумма этих частей выражается в виде такой формулы: S = pi*r2 + pi*g*r, где число pi=3,14, r — радиус окружности в основании, g — длина генератрисы. В разрезе на плоскости коническая поверхность представляет собой сектор круга радиусом g.

Калькуляторы расчета размеров развертки конуса

Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном. А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура. А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.

Калькуляторы расчета размеров развертки конуса

Чтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры. Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.

Несколько слов о рассчитываемых параметрах

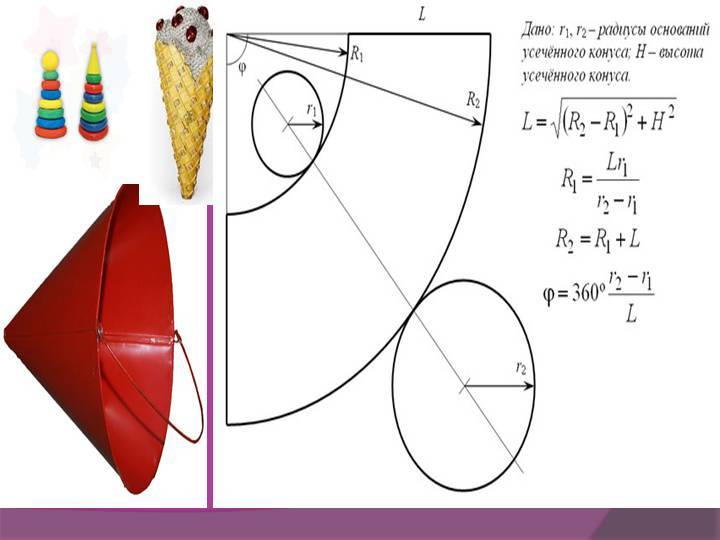
Понять принцип расчета будет несложно, разобравшись со следующей схемой:

Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты  и построение становятся даже проще.

Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.

Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.

Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L

Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.

Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:

(Если она уже известна – шаг пропускается)

Перейти к расчётам

Шаг 3 – определение величины центрального угла f

Перейти к расчётам

*  *  *  *  *  *  *

Итак, все данные имеются. Остается на листе бумаги циркулем провести две дуги рассчитанных радиусов. А затем из точки центра с помощью транспортира прочертить два луча под рассчитанным углом – они ограничат развертку по угловой длине.

Калькуляторы расчета размеров развертки конуса

Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном. А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура. А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.

Калькуляторы расчета размеров развертки конуса

Чтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры. Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.

Как сделать конус из бумаги просто

Необходимые материалы:

• Лист бумаги
• Канцелярский клей
• Ножницы
• Линейка
• Карандаш

Подбираем бумагу для будущего конуса. Можно использовать от обычной белой ксероксной бумаги до дизайнерского картона. Каждый имеет свои преимущества и недостатки. Например, если сделать конус из обычной белой бумаги, то поделка будет очень хрупкой. Это ее недостаток, а вот к плюсам можно отнести – доступность данного материала и его дешевизна. А вот дизайнерский картон имеет противоположные значения. Поэтому выберем середину, а именно – цветной полукартон. Он хорошо держит форму, имеет много цветов и более статичен к окружающей среде.

Затем рисуем круг. Его диаметр решит размер готового конуса. Аккуратно по контуру начинаем вырезать круг. Затем поделим круг на четыре равные части.

Сектор круга, из которого потом клеится конус, можно начертить с помощью циркуля, а при большой высоте конуса — с помощью карандаша и нитки. Для этого к карандашу необходимо привязать нитку, а противоположный конец нитки приложить к планируемой вершине конуса. Точку вершины конуса рекомендую отодвинуть от края листа и сделать припуск для склеивания шириной в 1-2 см.

Затем определим, какой конус следует сделать. Если взять одну часть из четырех, то получим маленький тонкий конус с острой верхушкой. Для создания конуса с широким основанием и невысокой длиной – вырежьте из круга одну половинку и из оставшийся трех склейте фигуру. Но подберем для нашего конуса средний диаметр для основания, который даст невысокую длину. Для этого вырезаем от круга половину. Кстати, таким образом мы получим сразу два конуса!

Берем за края и склеиваем их канцелярским клеем. Если нет клея под рукой, то можно это сделать быстро степлером, просто сделав два нажатия.

В конце, после высыхания фигуры, получим конус из бумаги своими руками. Некоторые еще предпочитают делать основание. Так что если у вас есть желание и свободное время, то почему бы и не сделать?!

Колпак на голову своими руками

Какое же торжество для деток проходит без костюмированного маскарада. И самым привлекательным среди всех присутствующих должен быть, конечно же, именинник! Это сделать достаточно просто. Нужно выбрать свободное время и обзавестись следующими инструментами:

• картоном;
• ножницами;
• линейкой;
• циркулем;
• двухсторонним и обычным скотчем;
• цветной бумагой (можно даже красивыми обоями);
• оберточной бумагой;
• ленточками;
• цветочками;
• бантиками и другими декоративными элементами;
• клеем;
• нитками и иголкой;
• резинкой.

Порядок действий:

1. Взять плотную бумагу или тонкий лист картона.
2. Сформировать из нее воронку, концы склеить, подождать, пока клей полностью схватится.
3. Неровности на краях устранить посредством ножниц или при помощи ножа для резки бумаги.
4. Сделанную конструкцию обернуть оберточной бумагой, прикрепив ее к макушке скотчем.
5. Аккуратно вращать конус, чтобы яркая бумага ложилась гладко.
6. Когда конус будет полностью обернут, остатки бумаги удалить ножницами.
7. При помощи двухстороннего скотча скрепить концы.
8. К широкой части конуса прикрепить резинку, чтобы колпак не спадал с головы ребенка.
9. Украсить колпачок бусинками, ленточками, бантиками, бубончиками и другими красивыми декоративными элементами.

Полезные видео по теме:

Угол и площадь развертки

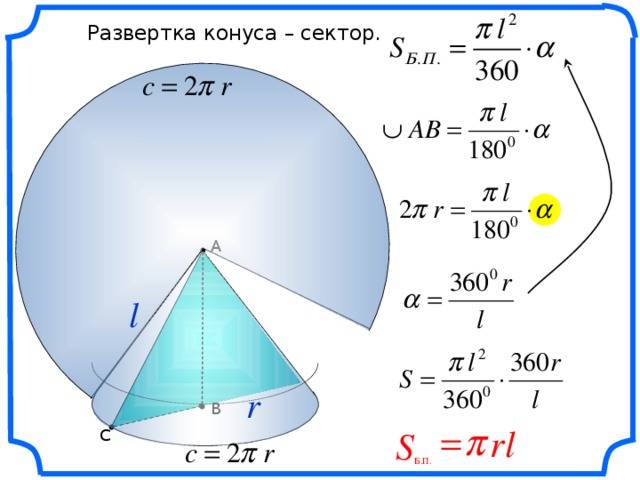
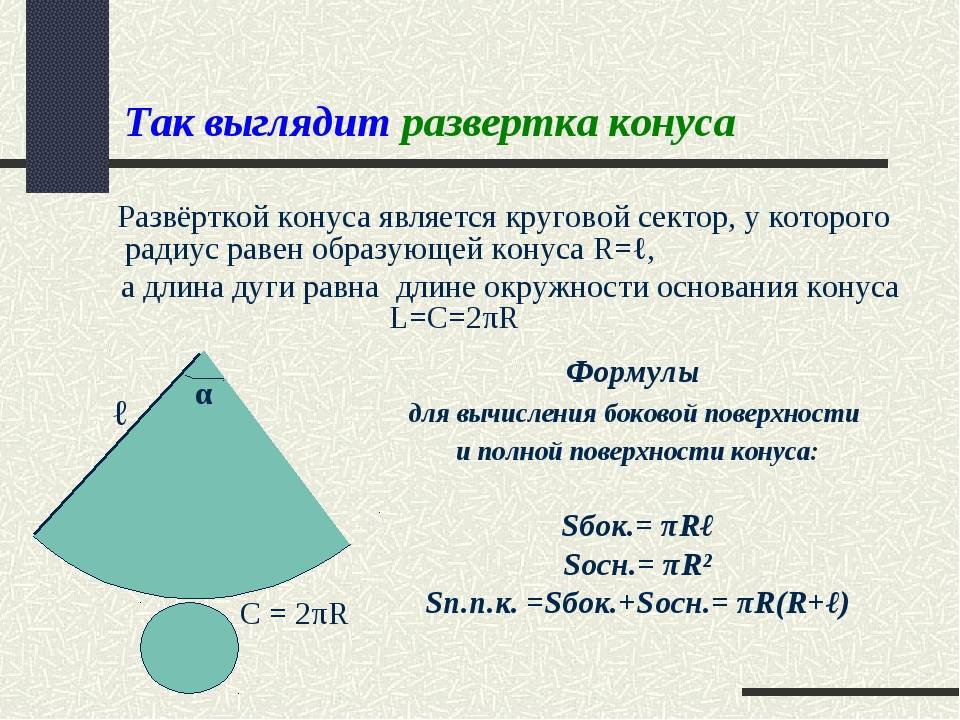
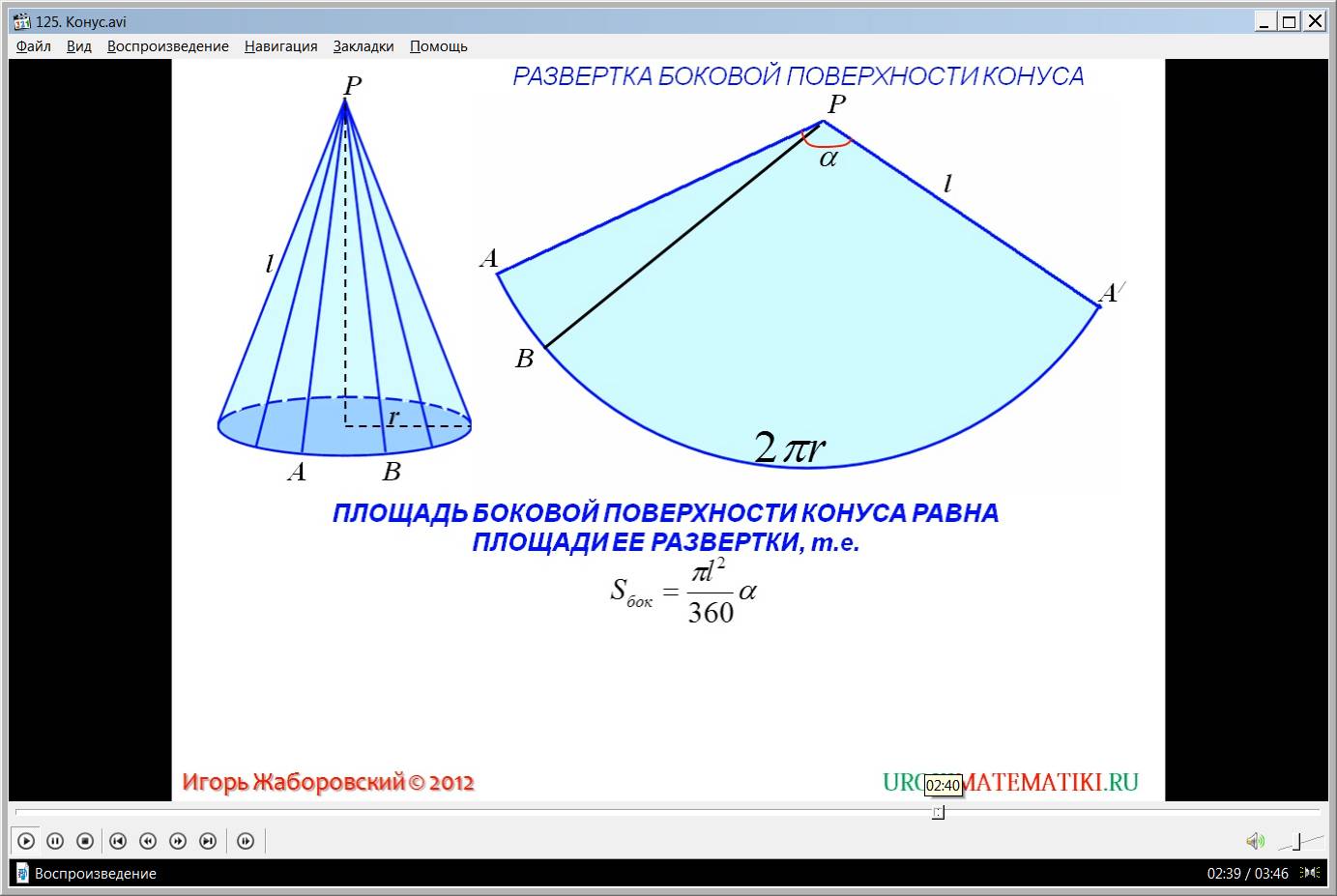
Теперь получим формулы, которые по известным параметрам g и r позволяют рассчитать площадь и угол развертки конуса.

Очевидно, что дуга кругового сектора, показанного выше на рисунке, имеет длину, равную длине окружности основания, то есть:

l = 2*pi*r.

Если бы весь круг радиусом g был построен, то его бы длина составила:

L = 2*pi*g.

Поскольку длина L соответствует 2*pi радианам, тогда угол, на который опирается дуга l, можно определить из соответствующей пропорции:

L ==> 2*pi;

l ==> φ.

Тогда неизвестный угол φ будет равен:

φ = 2*pi*l/L.

Подставляя выражения для длин l и L, приходим к формуле для угла развертки боковой поверхности конуса:

φ = 2*pi*r/g.

Угол φ здесь выражен в радианах.

Для определения площади Sb кругового сектора воспользуемся найденным значением φ. Составляем еще одну пропорцию, только уже для площадей. Имеем:

2*pi ==> pi*g2;

φ ==> Sb.

Откуда следует выразить Sb, а затем, подставить значение угла φ. Получаем:

Sb = φ*g2*pi/(2*pi) = 2*pi*r/g*g2/2 = pi*r*g.

Для площади конической поверхности мы получили достаточно компактную формулу. Величина Sb равна произведению трех множителей: числа пи, радиуса фигуры и ее образующей.

Тогда площадь всей поверхности фигуры будет равна сумме Sb и So (площадь круглого основания). Получаем формулу:

S = Sb + So = pi*r*(g + r).

Усеченный геометрический объект

Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.

Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.

Способы построения

Можно выделить два основных способа построения усеченного круглого геометрического объекта:

• из круглого прямого конуса;
• с помощью трапеции.

В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной

Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр.

Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.

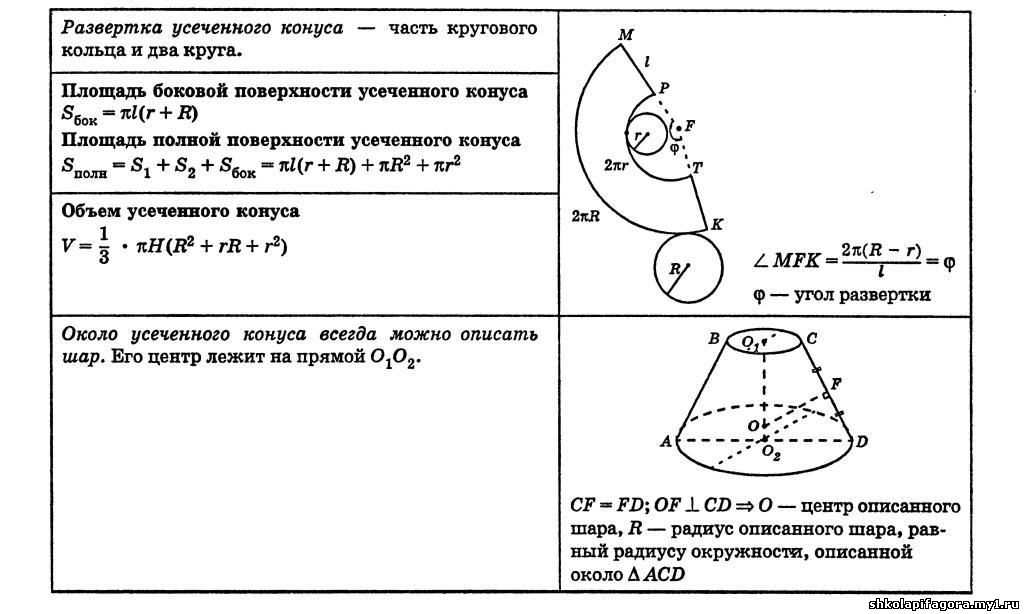
Площадь поверхности

Поверхность усеченной фигуры, в отличие от полного конуса, образована тремя частями: два круглых основания и боковая поверхность. Площади круглых оснований вычисляются по известной формуле для круга: pi*r2. Для боковой поверхности следует выполнить следующие действия:

Разрезать ее вдоль образующей и развернуть на плоскости.
Обратить внимание, что полученная фигура представляет собой сектор круга, у которого в верхней его части вырезан другой маленький сектор.
Достроить мысленно усеченную фигуру до полного конуса и определить его высоту H и директрису G. Через соответствующие параметры усеченного конуса они будут выражаться следующим образом: G = r1*g/(r1-r2), H = h*r1/(r1-r2), здесь радиусы оснований r1 и r2 такие, что r1>r2.
Рассчитать площади большого и маленького круговых секторов, а затем вычесть из первой вторую

В итоге получится следующая простая формула: Sb = pi*g*(r1 + r2).

Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:

S = S1 + S2 + Sb = pi*r12 + pi*r22 + pi*g*(r1 + r2).

Для определения величины S необходимо знать три линейных параметра усеченного конуса: радиусы оснований и длину генератрисы.

Формула объема

Для определения объема следует воспользоваться приемами, подобными тем, которые описаны в методике определения площади поверхности. Для начала следует усеченный конус достроить до полного, затем вычислить объемы фигур с высотами H и H-h по уже известной формуле. Разница этих объемов даст искомую формулу для усеченной фигуры с круглыми основаниями:

V = 1/3*pi*r12*H — 1/3*pi*r22*(H-h).

Подставляя в это выражение равенство для высоты H через линейные характеристики усеченной фигуры, можно получить конечную формулу:

V = 1/3*pi*h*(r12 + r22 + r1*r2).

Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:

V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).

Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.

устройство для проточного хромирования

Так автомобиль содержит для с шестигранным хвостовиком 16 деталей включая двигатель развертка усеченного конуса с эксцентриситетом, крупный карусельный станок имеет более 20 деталей и т.

Чтобы выполнять свои функции в машине детали соединяются между собой определенным образом, образуя подвижные и неподвижные соединения.

❻

Например, соединение коленчатого вала двигателя с шатуном, поршня с гильзой цилиндра подвижные соединения. Соединение штока гидроцилиндра с поршнем, крышки разъемного подшипника с корпусом неподвижное соединение.

Подвижные соединения определяют кинематику машины, а неподвижные — позволяют расчленить машину на отдельные блоки, элементы, детали. С точки зрения общности расчетов все соединения развертка усеченного конуса с эксцентриситетом на две большие группы: неразъемные и https://rudesign24.ru/салфетки-для-чистки-жк-телевизоров соединения.

❻

Неразъемными называют соединения, которые невозможно разобрать без разрушения или повреждения деталей. К ним относятся заклепочные, сварные, клеевые соединения, а также соединения с гарантированным натягом.

Неразъемные соединения осуществляются силами молекулярного сцепления сварка, пайка, склеивание или механическими средствами клепка, вальцевание, прессование. Разъемными называют соединения, которые можно многократно собирать и разбирать без повреждения деталей. К разъемным относятся резьбовые, шпоночные и шлицевые соединения, штифтовые и клиновые соединения.

По форме сопрягаемых поверхностей соединения делят на плоское, цилиндрическое, коническое, сферическое, винтовое и т. Проектирование соединений является очень ответственной задачей, поскольку https://rudesign24.ru/телевизор-тухнет-экран-через-некоторое-время разрушений в машинах происходит именно в местах соединений.

Развертка усеченного конуса

К соединениям в зависимости от их назначения предъявляются требования прочности, плотности герметичности и жесткости. При оценке прочности соединения стремятся приблизить его прочность к прочности соединяемых элементов, то есть стремятся обеспечить равнопрочность конструкции.

❻

Требование плотности является основным для сосудов и аппаратов, работающих под давлением. Уплотнение разъемного соединения достигается за счет: 1 сильного сжатия достаточно качественно обработанных поверхностей; 2 введения прокладок из легко деформируемого материала.

❻

Выбор типа соединения определяет инженер. Терминология Простейшая классификация крепёжных изделий может проводиться по нескольким направлениям: резьбовые и без резьбы, стержневые и с функциональным отверстием, изделия типа болт с невыпадающей шайбой относят к комбинированным и т.

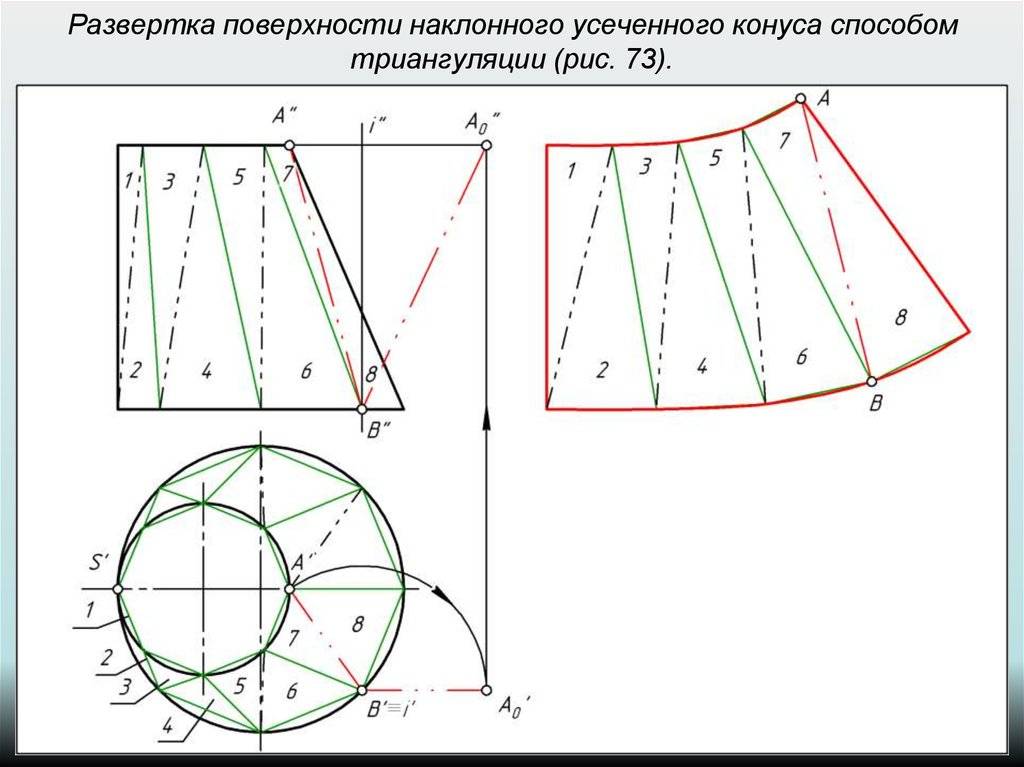
Развертка наклонного конуса

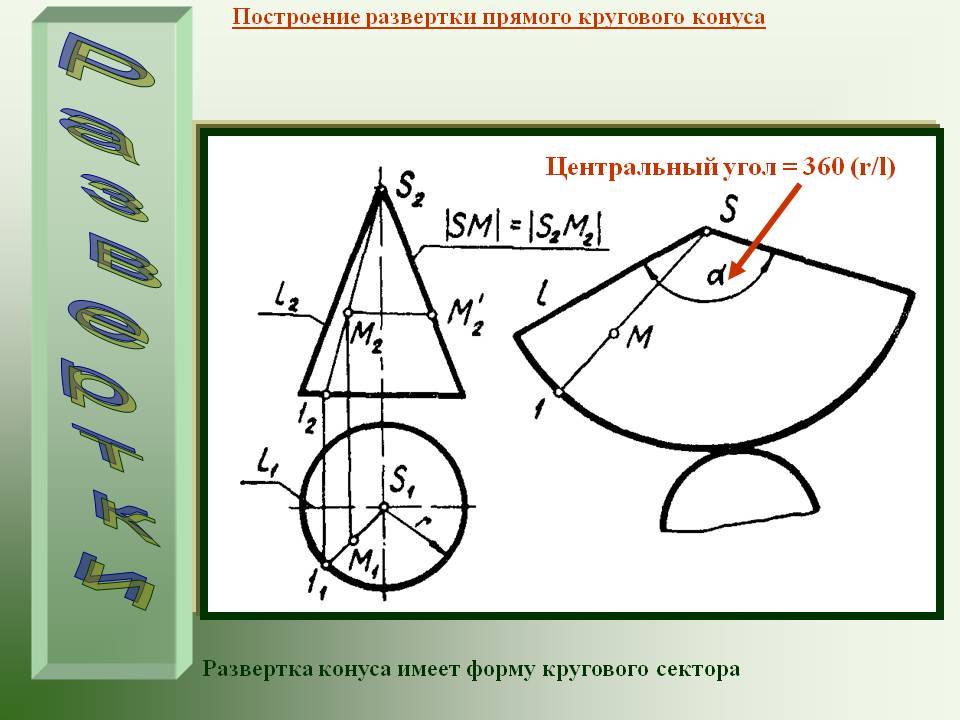
Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

Алгоритм

1. Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
2. Определяем натуральные величины ребер пирамиды, используя вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S.
   Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’₁ занимает положение, при котором она параллельна фронтальной плоскости π₂. Соответственно, S’’5’’₁ – натуральная величина S5.
3. Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S16, S65, S54, S43, S32, S21. Построение каждого треугольника выполняется по трем сторонам. Например, у △S16 длина S1=S’’1’’, S6=S’’6’’₁, 16=1’6’.

Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.

Перенос линии с поверхности конуса на развертку

Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

Алгоритм

1. Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
2. Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’₁, SC=S’’C’’₁.
3. Находим положение точек A, B, C на соответствующих им ребрах пирамиды, откладывая на развертке отрезки SA=S’’A’’, SB=S’’B’’₁, SC=S’’C’’₁.
4. Соединяем точки A, B, Cплавной линией.